함수에 이어서 재귀로~
함수(Function)란 하나의 특별한 목적을 가진 작업을 수행하기 위해 독립적으로 설계된 코드의 집합으로 정의할 수 있습니다. 함수를 선언하려면 일정한 문법적인 규칙을 지켜야 하기 때문에 매개 변수나 리턴에 대한 이해가 필요합니다.
함수를 처음 배울 때는 실제로 매개 변수를 넘겨주고, 함수의 리턴 값을 출력해 보는 연습을 하면서 함수에 대한 개념을 이해합니다. 함수를 이해했다면, 재귀로 넘어가게 되는데, 재귀를 이해한다면 함수를 정의한 후 재사용하는 것에 대한 내용을 더 깊이 이해하며, 컴퓨팅 사고력을 향상 시킬 수 있습니다.
재귀, 되었다고 믿어라.
재귀를 수업할 때는 되었다고 믿어야 합니다.
처음 상태와 관계식을 구현하고 끝을 정해 놓으면 다 됩니다.
하지만 막상 이렇게 생각하는 건 쉽지 않습니다. 그래서 정말 그런가…하며 하나씩 값을 따라가 보기도 하는데, 실제로 값을 따라가며 출력 값을 확인해 보면 잘 동작하고 있다는 것을 확인할 수 있습니다. 쉽지 않지만, 한 번 이해하게 된다면 굉장히 매력적인 구현 방법입니다.
잘 하려면 많이 구현해 보며 익숙해져야 합니다.
파스칼의 삼각형을 재귀로 구현하기
파스칼의 삼각형이란?
수학에서 이항계수를 삼각형 모양의 기하학적인 형태로 배열한 것입니다.
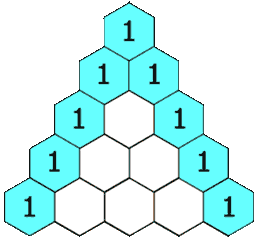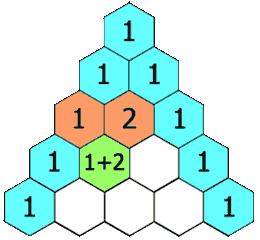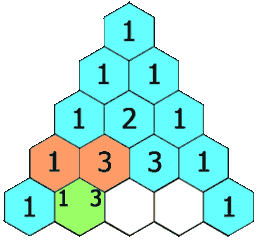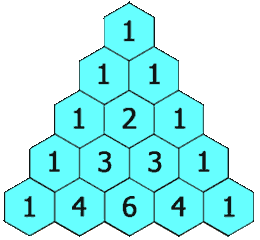
파스칼의 삼각형 다음과 같이 단순한 형태로 만들 수 있습니다.
먼저 첫 번째 줄에는 1을 적어 줍니다.
그 다음 줄을 만들기 위해서는 바로 왼쪽 위의 숫자와 오른쪽 숫자를 더해야 합니다. 만약 바로 위의 숫자가 4와 6이었다면 그 아래의 숫자는 10이 되는 것이죠. 이러한 과정을 통해서 파스칼의 삼각형을 완성할 수 있습니다.
파스칼의 삼각형의 기본 공식은 nCm = n-1Cm + n-1Cm-1입니다.
공식을 간단히 설명하자면, n을 5, m을 3이라 할 때 5명 중에서 3명을 뽑을 확률은 5명 중 특정한 A가 3명 안에 뽑히지 않는 경우와 A가 3명 안에 뽑히는 경우의 합과 같다는 의미가 됩니다.
3명 중 A가 뽑히지 않았다면, 나머지 4명 중 3명을 뽑는 경우의 수는 4C3, 3명 중 A가 뽑혔다고 한다면 나머지 4명 중 2명을 뽑는 경우의 수는 4C2이 됩니다. 따라서 5C3 = 4C2 + 4C3이 성립하게 되는 것입니다.
재귀 함수를 코딩할 때 가장 중요한 것은 반복이 끝나는 지점을 확실하게 정하는 것입니다.
함수의 특성상 자칫 잘못 코딩하면 재귀 함수에서 빠져나오지 못한 채 끝없이 반복을 하게 되기 때문에 이 함수가 어떻게 흘러가는지, 어느 지점에서 정해진 리턴 값을 주어야 하는지, 예상치 못한 이유로 재귀를 멈춰야 할 지점을 지나치지는 않는지 잘 생각해서 코딩해야 합니다.
그렇다면 이 함수는 언제 재귀를 멈추고 정해진 값을 리턴해야 할까요?
조합의 성질에 따르면 nC0, 즉 n명 중에서 0명을 뽑는 경우의 수는 0이므로 m == 0일 경우 0을 리턴해야 합니다. 또한 nCm = nCn-m이므로 nC0 = nCn-0 = nCn이 됩니다. 따라서 n == m인 경우도 0을 리턴합니다. 그 이외의 경우에는 파스칼의 삼각형 공식에 따라 n-1Cm + n-1Cm-1 를 리턴합니다.
코드
보통의 경우 앞의 문제는 m이 0이 되고, 뒤의 문제는 n이 m과 같아지면서 반복이 끝나지만 m이 음수이거나 m이 n보다 큰 경우 반복이 끝나지 않습니다. 이를 해결하기 위해서는 아래와 같은 예외 코드를 작성해야 합니다.
int Combi(int n, int m) {
if (m == 0 || m == n) {
return 1;
}
else if (m < 0 || n < m){
return 0;
}
else {
return Combi(n-1, m-1) + Combi(n-1, m);
}
}
C
복사