안녕하세요? 이번 달 PS문제는 고등학교 정보 3단원에서 활용할 수 있는 ‘이진탐색’ 알고리즘입니다.
컴퓨터 과학에서 정렬과 탐색은 가장 기본적이면서 중요한 알고리즘입니다. 컴퓨터는 한정된 자원인 시간과 메모리 등을 효율적으로 이용하여 문제를 해결해야 하는데 정렬과 탐색은 알고리즘의 효율성을 비교적 쉽게 이해할 수 있는 알고리즘으로, 고등학생들도 이해하기 쉬운 예시로 활용됩니다.
그럼 지금부터 탐색과 관련된 아래 나무 자르기 문제를 풀어보고 수업에 꼭 활용해 보시길 바랍니다
문제 설명
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해 버렸기 때문에 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내 주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할 것이다.
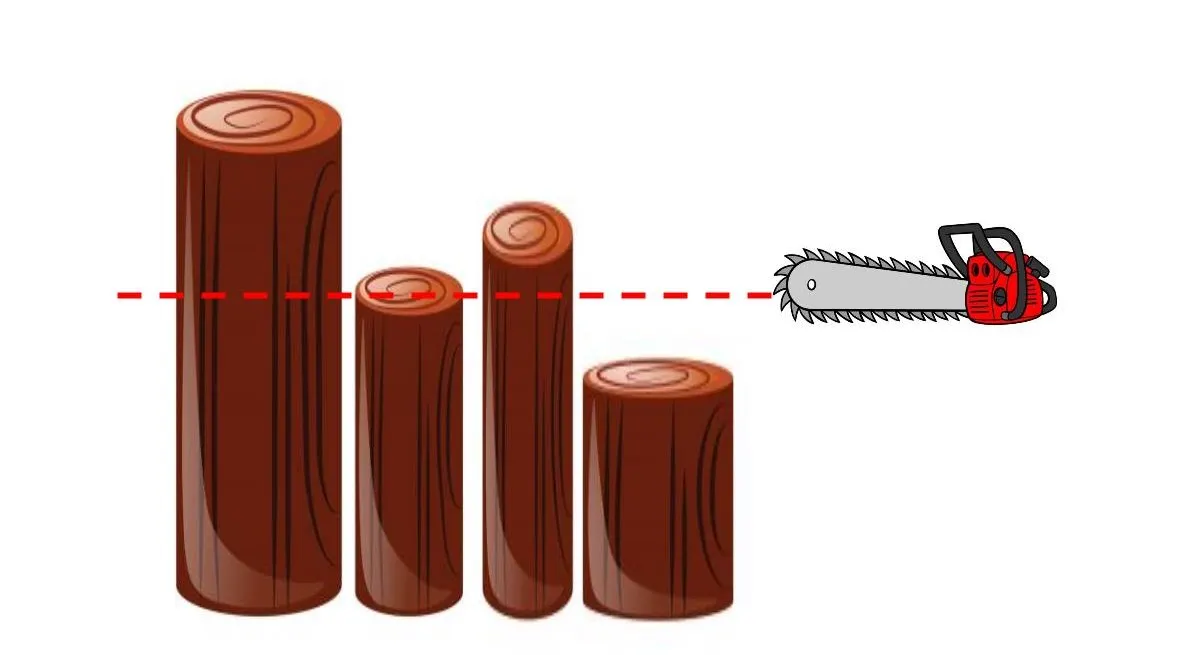
목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라가며 한 줄에 연속해 있는 나무를 모두 절단해 버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해 있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다.(총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다.
(1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
예시
4 7
20 15 10 17
Plain Text
복사
출력
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
예시
15
Plain Text
복사
문제 이해 및 분석
•
문제에서 해결하고자 하는 것은?
: 적어도 M미터의 나무를 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값
•
문제의 현재 상태와 목표 상태는?
◦
현재 상태 : 나무의 수(N)와 상근이가 집으로 가져가려고 하는 나무의 길이(M)가 주어짐
◦
목표 상태 : M미터의 나무를 집에 가져가기 위해 절단기에 설정할 높이를 구하려고 함
알고리즘 설계 및 프로그래밍(순차탐색)
효율적인 풀이가 바로 떠오르지 않는다면 컴퓨터에게 하나씩 찾아보도록 시켜보는 것도 좋은 방법이다. 문제에서 구하고자 하는 것이 절단기에 설정할 수 있는 높이의 최댓값이므로 나무 높이의 최대값(i라 하자)부터 시작하여 1씩 줄여가면서 처음으로 M이 넘는 i를 찾으면 끝난다.
#제일 큰 나무 높이부터 하나씩 줄여가며 순차탐색
N, M = map(int, input().split())
trees = list(map(int, input().split()))
i = max(trees)
sum = 0
while sum < M :
i -= 1
sum = 0
#정해진 i로 자르고 남는 합 구하기
for j in trees :
if j > i :
sum += (j - i)
print(i)
Python
복사
위와 같은 순차탐색을 활용한 문제 해결 방법은 ‘시간 초과’가 나올 것이다.
순차탐색의 시간복잡도는 O(N)이며, 높이(N의 범위)는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다. 입력값의 최댓값은 10억이고, 이를 고려하여 반복문은 제시된 시간 제한 ‘1초’를 넘겨버린다.
※ 1억 번 연산하는데 약 1초 정도 걸린다.
따라서, 순차탐색보다 효율적인 이진탐색 O(logN)을 활용해야 한다.
알고리즘 설계 및 프로그래밍(이진탐색)
이진탐색은 업&다운 게임과 유사하다.
(누군가 1~100 숫자 중에서 자신이 생각해둔 숫자를 5번 안에 맞춰보라고 하면 사람 심리상 반을 버릴 수 있는 50을 외치게 되어 있다.)
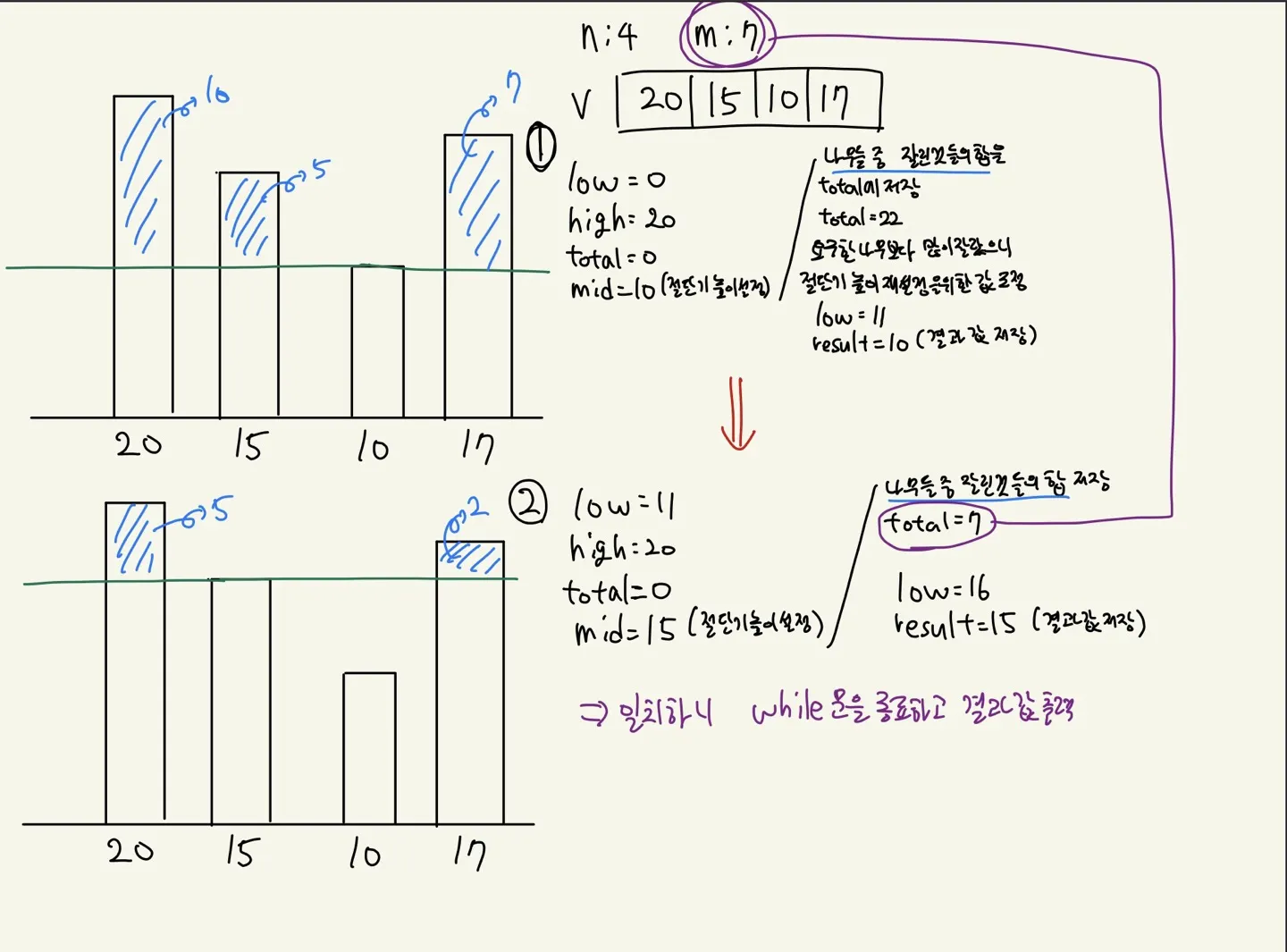
위 나무 자르기 예시에서 start를 0, end를 20(나무 max값)으로 두고 그 가운데 값인 10을 mid로 두어 나무를 잘라보고 M이 넘는지 확인한다.
나무를 자른 합이 M을 넘는다면 우선 높이를 result에 저장해 둔다. 절단 높이를 더 높여도 M이 넘을 수도 있으니 mid+1에서 20을 새로운 시작과 끝으로 정해 탐색을 반복한다.
나무를 자른 합이 M을 넘지 않는다면 더 많이 잘라야 하므로 0에서 mid-1를 새로운 시작과 끝으로 정해 탐색을 반복한다.
#이진탐색 이용
N, M = map(int, input().split())
trees = list(map(int, input().split()))
end = max(trees)
start = 0
while start <= end :
mid = (start + end)//2
sum = 0
#정해진 mid로 자르고 남는 합 구하기
for i in trees :
if i > mid :
sum += (i - mid)
#탐색 범위 조정하기
if sum >= M :
result = mid
start = mid + 1
else :
end = mid - 1
print(result)
Python
복사
⇒ 결국, 나무를 자른 후에 합계가 요구 나무 길이(M)과 동일한지 확인을 하는 것이 핵심이다!
하지만, 제일 큰 나무 길이부터 차례대로 자르는 것은 너무 오래 걸리기 때문에 이진탐색으로 찾자!
같은 방법을 C++로 해결하면 다음과 같다.
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> v;
int n, m, vn;
int result, mid;
long long int total;
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> vn;
v.push_back(vn);
}
int low = 0;
// 탐색의 범위 중 큰 값은 int high = 1e9; 와 같이 큰 값을 넣어도 되지만,
// 입력된 벡터 내에 큰 값을 반환하게끔 하였다.
// max_element를 위해 #include<algorithm> 를 하였고,
// iterator의 값을 반환하기 위해 *를 활용하였다.
int high = *max_element(v.begin(),v.end());
// 이분 탐색 시작.
while (low <= high)
{
total = 0;
mid = (low + high) / 2;
for (int i = 0; i < n; i++)
{
// mid라는 변수를 기준으로 나무가 잘렸다면,
// 자른 길이를 total이라는 변수에 담아둔다.
if (v[i] > mid)
total += v[i] - mid;
}
// 요구한 나무개수에 따라서 탐색 범위를 조정한다.
if (total < m) // 나무가 부족한 경우
high = mid - 1;
else //나무가 충분함.
{
result = mid;
low = mid + 1;
}
if(result == m)
break;
}
cout << result;
}
C++
복사